
SCILAB DERIVATIVE CODE
Given a Scilab code computing a variable y. Acceleration is the second derivative of the position function. Description : This toolbox enables Scilab code differentiation using operators and primitive functions overloading. Velocity is the first derivative of the position function.Is velocity the first or second derivative?.If you are dealing with compound functions, use the chain rule. multipliers and divisors), derive each component separately, carefully set the rule formula, and simplify. To calculate derivatives start by identifying the different components (i.e.Will keep you updated on future developments. The module is still a work in progress and I’m working on more functionalities to calculate the more roots simultaneously.Īnyone is welcome to contribute to this project. It can even find complex roots if the inital guess is complex.

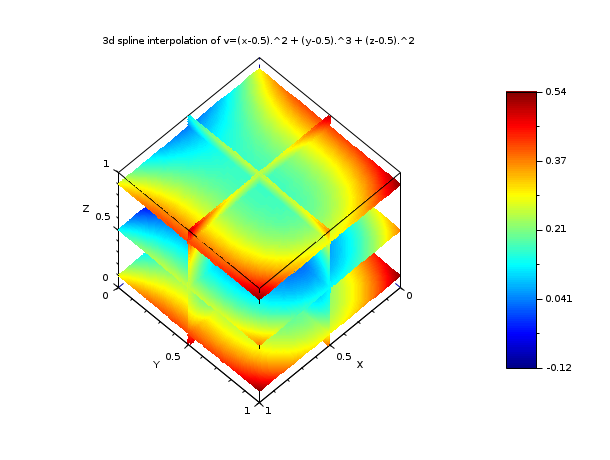
One of the functions in the modules uses Newton-Raphson Method which is the best availabe function to find the roots available in the toolbox. They only return a single root at a time and one needs to change the initial values for different roots. Numerical Methods are iterative methods that rely on an initial guess to find the exact root. License: Creative Commons Attribution-ShareAlike 3.0Ī brand new #scilab Module created by me that lets you find the root of any algebraic or transcendental equation by Numerical Methods. Summary: A toolbox with various functions for finding the roots of various algebraic or transcendental equations using Numerical Techniques. NOTE: The above functions never return all the root of the equation so you can adjust the initial guess that you give as arguments to get the different roots. However to use the Newton-Raphson Method, you will also need to provide the derivative of the equation, so define a function ‘df’ which is the derivative ‘f’: deff('a=df(x)','27*x^2') Īnd then call the nrsolve() which will return a root. derivatives can often by gotten by using the Scilab function derivative. Then all you need to do is, first define a function: deff('a=f(x)','a=9*x^3-81')Īnd then simply use the function, bsolve, sesolve as follows: bsolve(0,5,f,0.0000001) 4.7.1 Higher Derivatives Sometimes it is desirable to have higher derivatives. Scicos, a hybrid dynamic systems modeler. Suppose you want to find a root of the equation “9x^3-81”. directly used in Scilab with the help of the Matlab to Scilab translator. You can load help by typing “help eqnsolver” in the Scilab console. There are help pages for each of the function. Using the toolbox is pretty straight-forward. quadsolver – Finds the roots of a quadratic polynomial.(See help derivat. We will choose x between 0 and 1 with an increment of 0.001. In Scilab symbolic differentiation is only possible for polynomial or rational matrices w.r.t. We’ll do this by using the Scilab function deff (): deff ('yprimf (x,y)','yprim (x+1)/y') Second, we will define the values of x for which we want to compute the solution of the differential equation. bsolve – Finds the root of an equation within a given interval using the Bisection Method To find the numeric solution, first, we need to define our differential equation.sesolve – Finds the root of an equation using a Numerical Technique called Secant Method.Before getting into the details, we briefly motivate the need for. In this version, we have added some more lines which we explain separately. nrsolve – Finds the real or complex root of an equation using a Numerical Technique called Newton-Raphson Method. In this document, we analyse the computation of the numerical derivative of a given function. the topological derivative in addition to the shape derivative.There are 4 functions available for now, but I am still working on this toolbox so I may add a few more. The equation can be transcendental or algebraic. the rst derivative when the variable x is a simple scalar. The most simple calling sequence of this function is J derivative ( F, x ) where F is a given function, x is the point where to compute the derivative and J is the Jacobian, i.e. ‘eqnsolver’ is a SCILAB toolbox that provides various functions to estimate the root of any equation by Numerical Methods. In order to compare our results, we use the derivative function provided by Scilab.


 0 kommentar(er)
0 kommentar(er)
